Équation de Callendar-Van Dusen (CVD)
La relation entre la température et la valeur ohmique des RTD a été calculée par Callendar puis, plus tard, affinée par Van Dusen; c’est pourquoi cette équation est nommée Callendar-Van Dusen.
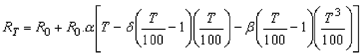
Avec RT = résistance à T°C, R0 = résistance à 0°C, α = coefficient de température à 0°C en Ω/Ω/°C, δ = coefficient de linéarisation, β = deuxième coefficient de linéarisation pour les valeurs négatives de température (β = 0 pour T > 0°C).
Cette équation a été transformée pour pouvoir être utilisée plus facilement avec les coefficients A, B et C donnés par la norme DIN 43760 (IEC 751) et les fiches techniques des composants :
Avec les conversions suivantes:
Ces trois valeurs α représentent les trois principales spécifications pour les RTD..
- 0,003850 Ω/Ω/°C : Normalisation DIN 43760, IEC 751 et autres spécifications internationales, nommé Standard Européen.
- 0,003926 Ω/Ω/°C : Nécessite un platine pur à 99,999% ou mieux, nommé Standard Américain.
- 0,3911 Ω/Ω/°C : Souvent nommé Standard Industriel U.S.
L’équation de Callendar-Van Dusen permet une bonne linéarisation des RTD, ± 0.01°C entre -100°c et +100°C mais l’erreur augmente rapidement avec les hautes températures. De plus, cette équation calcule la résistance en fonction de la température ; ce qui est l’inverse des utilisations les plus courantes : température en fonction de la résistance.
Pour convertir la valeur de résistance du RTD en température, on est obligé d’utiliser une équation quadratique du 2e degré, qui est, en quelque sorte, la réciproque de l’équation Callendar-Van Dusen, mais uniquement pour les températures supérieures à 0°C.
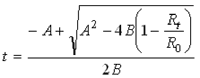
Pour les températures inférieures à 0°C, l’équation Callendar-Van Dusen est trop complexe à résoudre, aussi l’emploi des approximations successives s’impose
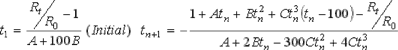
La table suivante nous propose des valeurs calculées avec l’équation de Callendar-Van Dusen
On peut voir que les écarts de l’équation CVD sont limités et situés aux environs de 0,05% et de 0,1% pour les hautes températures.
Équation de Callendar-Van Dusen (CVD)
La relation entre la température et la valeur ohmique des RTD a été calculée par Callendar puis, plus tard, affinée par Van Dusen; c’est pourquoi cette équation est nommée Callendar-Van Dusen.
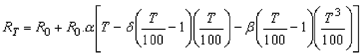
Avec RT = résistance à T°C, R0 = résistance à 0°C, α = coefficient de température à 0°C en Ω/Ω/°C, δ = coefficient de linéarisation, β = deuxième coefficient de linéarisation pour les valeurs négatives de température (β = 0 pour T > 0°C).
Cette équation a été transformée pour pouvoir être utilisée plus facilement avec les coefficients A, B et C donnés par la norme DIN 43760 (IEC 751) et les fiches techniques des composants :
Avec les conversions suivantes:
Ces trois valeurs α représentent les trois principales spécifications pour les RTD..
- 0,003850 Ω/Ω/°C : Normalisation DIN 43760, IEC 751 et autres spécifications internationales, nommé Standard Européen.
- 0,003926 Ω/Ω/°C : Nécessite un platine pur à 99,999% ou mieux, nommé Standard Américain.
- 0,3911 Ω/Ω/°C : Souvent nommé Standard Industriel U.S.
L’équation de Callendar-Van Dusen permet une bonne linéarisation des RTD, ± 0.01°C entre -100°c et +100°C mais l’erreur augmente rapidement avec les hautes températures. De plus, cette équation calcule la résistance en fonction de la température ; ce qui est l’inverse des utilisations les plus courantes : température en fonction de la résistance.
Pour convertir la valeur de résistance du RTD en température, on est obligé d’utiliser une équation quadratique du 2e degré, qui est, en quelque sorte, la réciproque de l’équation Callendar-Van Dusen, mais uniquement pour les températures supérieures à 0°C.
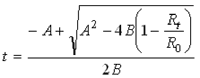
Pour les températures inférieures à 0°C, l’équation Callendar-Van Dusen est trop complexe à résoudre, aussi l’emploi des approximations successives s’impose
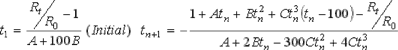
La table suivante nous propose des valeurs calculées avec l’équation de Callendar-Van Dusen
On peut voir que les écarts de l’équation CVD sont limités et situés aux environs de 0,05% et de 0,1% pour les hautes températures.








