Callendar-Van-Dusen (CVD) Equation
The relationship between the temperature and ohmic value of RTD’s were calculated by Callendar, and later on, refined by Van Dusen; this is why the equation is named Callendar-Van Dusen.
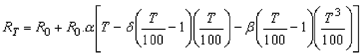
With RT = resistance at T°C , R0 = resistance at 0°C, = temperature coefficient at 0°C in //°C, = linearisation coefficient, = second coefficient of linearisation for negatives temperature values ( = 0 for T > 0°C).
This equation has been transformed in order to be used easily with the coefficients A, B and C given by the standard DIN 43760 (IEC 751) and the component technicals specifications with the following conversions:
With the following conversions:
These three values represent the three principal specifications for RTD’s.
- 0,003850 //°C: Standard DIN 43760, IEC 751, named Europeen Industrial Standard.
- 0,003926 //°C: Require pur platinum (99,999%), named U.S. Industrial Standard.
- 0,3911 //°C: Often named U.S. Industrial Standard.
The Callendar-Van Dusen equation permits a good linearity of RTD’s, ±0.01°C between -100°C and +100°C but the error increases rapidly with high temperatures. Furthermore, this equation calculates the resistance with temperature change; which is the opposite of the most current uses : Temperature with resistance change.
To convert the resistance value of the RTD to temperature, we are obliged to use a quad equation to the 2nd degree, which is, in sort, the reciprocal of the Callendar-Van Dusen equation, but iniquely for temperatures superior to 0°C.
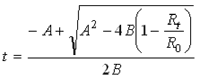
For temperatures inferior to 0 C, the Callendar-Van Dusen equation is too complex to reslove and the the use of successive approximations is necessary:
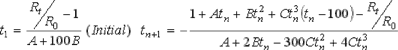
The following table propose calculated values with the Callendar-Van Dusen equation.
We can see that the gaps of the Callendar-Van Dusen equation are limited and are found around 0,05% and 0,1% for higher temperatures.
Callendar-Van-Dusen (CVD) Equation
The relationship between the temperature and ohmic value of RTD’s were calculated by Callendar, and later on, refined by Van Dusen; this is why the equation is named Callendar-Van Dusen.
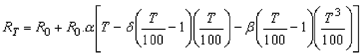
With RT = resistance at T°C , R0 = resistance at 0°C, = temperature coefficient at 0°C in //°C, = linearisation coefficient, = second coefficient of linearisation for negatives temperature values ( = 0 for T > 0°C).
This equation has been transformed in order to be used easily with the coefficients A, B and C given by the standard DIN 43760 (IEC 751) and the component technicals specifications with the following conversions:
With the following conversions:
These three values represent the three principal specifications for RTD’s.
- 0,003850 //°C: Standard DIN 43760, IEC 751, named Europeen Industrial Standard.
- 0,003926 //°C: Require pur platinum (99,999%), named U.S. Industrial Standard.
- 0,3911 //°C: Often named U.S. Industrial Standard.
The Callendar-Van Dusen equation permits a good linearity of RTD’s, ±0.01°C between -100°C and +100°C but the error increases rapidly with high temperatures. Furthermore, this equation calculates the resistance with temperature change; which is the opposite of the most current uses : Temperature with resistance change.
To convert the resistance value of the RTD to temperature, we are obliged to use a quad equation to the 2nd degree, which is, in sort, the reciprocal of the Callendar-Van Dusen equation, but iniquely for temperatures superior to 0°C.
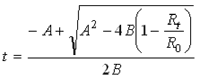
For temperatures inferior to 0 C, the Callendar-Van Dusen equation is too complex to reslove and the the use of successive approximations is necessary:
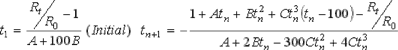
The following table propose calculated values with the Callendar-Van Dusen equation.
We can see that the gaps of the Callendar-Van Dusen equation are limited and are found around 0,05% and 0,1% for higher temperatures.







